Yahoo! employees Leonid Zhukov and Pavel Berkhin, and Stanford University searcher David Gleich (while working at Yahoo!) published a paper called "".

Here is the abstract:

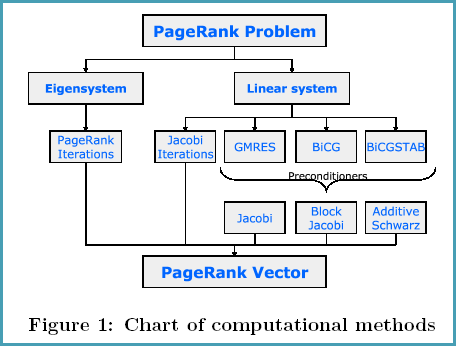
In this paper we investigate the convergence of iterative stationary and Krylov subspace methods for the PageRank linear system, including the convergence dependency on teleportation. We demonstrate that linear system iterations converge faster than the simple power method and are less sensitive to the changes in teleportation.

In order to perform this study we developed a framework for parallel PageRank computing. We describe the details of the parallel implementation and provide experimental results obtained on a 70-node Beowulf cluster.

And the conclusion:

In this paper we have demonstrated that PageRank can be successfully computed using linear system iterative solvers. We have developed an efficient scalable parallel implementation and studied Jacobi and Krylov subspace iterative methods. Our numerical results show that GMRES and BiCGSTAB are overall the best choice of solution methods for PageRank class of problems and, for most graphs, provide faster convergence than power iterations. We have also demonstrated that the linear system PageRank can converge for much larger values of the teleportation coefficient c than standard power iterations.

Maybe with such improvements of PageRank calculation, Google is already updating the PageRank continuously, even if it doesn't update the PageRank displayed on the Google Toolbar...

Via Abakus